twitter,facebook,ins,youtube视频下载
磨针音视频转文字
磨针免费pdf转word
磨针微信定时发文件和消息
磨针c盘清理，任何场景都能释放几十G的空间
终于有时间来还债了。如果想知道自己的市场价值，最好的方法就是: 去面试。
蛮多人觉得刷大量题目是很必要的，但我遇到的面试官，大部分更着重在，过程的提问和分析问题能力。
之前的工作不常碰树的结构，很巧的是，面试刚好被要求实作相关的东西。当下我很诚实的说: "I'm not quite familiar. I'll try my best."。
很幸运的是，顺利拿到那次的offer。我觉得我唯一做对的的事，就是尽可能的阐述我知道的，然后和考官讨论。
面试官需要的是...之后可以一起合作的同事。所以刷题练习时的，不要局限于做出来，可以透过问自己一些基本的问题、延伸问题，避免见树不见林。
以下会拿一题leetcode 作为范例:
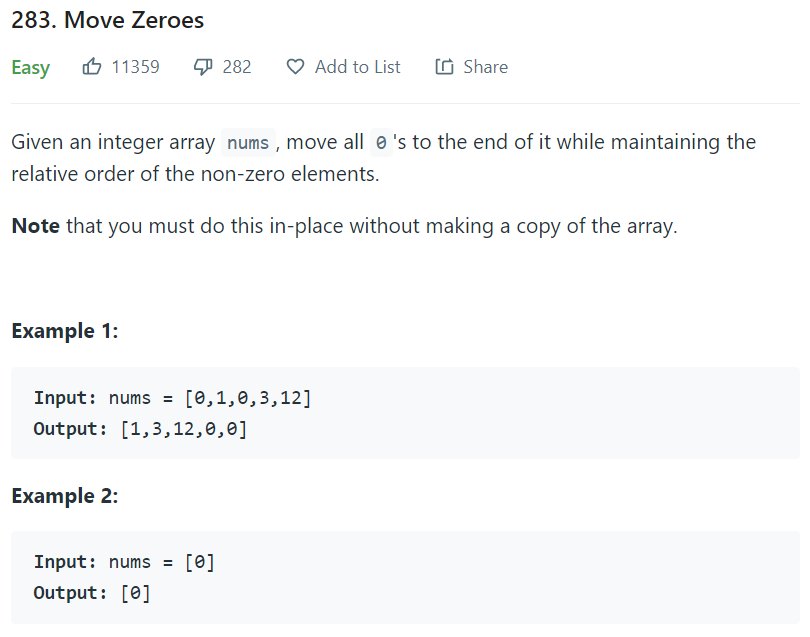
简单翻译，把阵列中的"0" 移到最前面，并且必须要以in-place 的方式来处理。
in-place algorithm 是指不产生额外的记忆体空间下，用时间换取空间。
所以心里有个底，这限制可能会影响时间复杂度。
既然要处理的是阵列，那这时需要确认基本的问题: 会遇到null 的array 吗? 会遇到负数吗? 除了0 之外的item 需不需要保留原本的顺序?
面试时提问可以限缩方向，刷题时提问可以让自己想得更多。
假设左边的顺序不影响，那么我会需要一个int 纪录交换的位置，然后利用一个for 回圈，去进行交换的动作。
到目前为止，都还没Coding。先动手的人就输了~
换个角度想，假设左边的顺序不影响，也不会出现负数，弄个快速排序(Quick sort) 也行阿! 这时零永远得在前面，后面的顺序没差~ 不过需要再反转一次~
这时候你需要知道: 什么是分而治之(Divide and conquer) ? 为何比同样原理、一样O(n log n)的合并排序还有效率?
跟面试官确认你要用哪个流程，接下来才是写程式跟测试。
上一下C# 的code，如果你不写C# 没关系，我会解释细节重点在哪:
- int 纪录交换位置+ for 回圈
(1) 方法的命名、程式码的排版，也会是加扣分的细节
(2) 纪录交换位置的switchIndex 不一定要从0 开始。不同题目有不同优势。
public void MoveZeroes(int[] arr)
{
int switchIndex = arr.Length;
for (int i = arr.Length-1; i >= 0; i--)
{
if (arr[i] == 0)
{
switchIndex--;
// array items 互換
int temp = arr[i];
arr[i] = arr[switchIndex];
arr[switchIndex] = temp;
}
}
return arr;
}
- 快速排序(In-place)
(1) 分而治之(Divide and conquer) 重点在递回的设计。找出什么时候是base case (最简单的情况也会是终止条件)，什么时候是recursive case (要继续)。
(2) 这边也可以使用Two-pointer 的技巧，有兴趣的人可看这边。他的系列文章统整得很好。
(3) 尽可能Clean code，有时候提出方法会让可读性变好。
public void MoveZeroes(int[] arr)
{
QuickSort(arr, 0, arr.Length - 1);
}
private void QuickSort(int[] arr, int start, int end)
{
int index;
if (start < end)
{
index = Partition(arr, start, end);
QuickSort(arr, start, index-1);
QuickSort(arr, index + 1, end);
}
}
private int Partition(int[] arr, int start, int end)
{
// 變數 temp 是交換用，這裡 pivot 取陣列的最右側
// pointer 紀錄換到哪
int temp;
int pivot = arr[end];
int pointer = start-1;
for (int i = start; i <= end-1; i++)
{
if (arr[i] < pivot)
{
pointer++;
temp = arr[i];
arr[i] = arr[pointer];
arr[pointer] = temp;
}
}
temp = arr[pointer+1];
arr[pointer+1] = arr[end];
arr[end] = temp;
return pointer + 1;
}
最后推荐几本中文书，真心好用，没有叶配: